8.4. Gradient Descent for Empirical Risk Minimization

While gradient descent can be used to (attempt to) minimize any differentiable function $f(\vec x)$ , we typically use it to minimize empirical risk functions, $R(\vec w)$ .

Let’s try using gradient descent to fit a linear regression model – that is, let’s use it to minimize

R_\text{sq}(\vec w) = \frac{1}{n} \lVert \vec y - X \vec w \rVert^2

This function has a closed-form solution, but it’s worthwhile to see how gradient descent works on it.

In Chapter 8.1, we found that the gradient of $R_\text{sq}(\vec w)$ is

\nabla R_\text{sq}(\vec w) = \frac{2}{n} (X^TX \vec w - X^T \vec y)

so, the update rule is

\vec w^{(t+1)} = \vec w^{(t)} - \alpha \frac{2}{n} (X^TX \vec w^{(t)} - X^T \vec y)

Let’s start by using gradient descent to fit a simple linear regression model to predict commute times in minutes from departure_hour – a problem we’ve solved many times.

We now apply gradient descent to empirical risk minimization.

import pandas as pd
import numpy as np
import plotly.express as px

df = pd.read_csv('data/commute-times.csv')
commutes_full = df

fig = px.scatter(
    df,
    x='departure_hour',
    y='minutes',
    size=np.ones(len(df)) * 50,
    size_max=8
)
fig.update_xaxes(
    title='Home Departure Time (AM)',
    gridcolor='#f0f0f0',
    showline=True,
    linecolor="black",
    linewidth=1,
)
fig.update_yaxes(
    title='Commute Time (Minutes)',
    gridcolor='#f0f0f0',
    showline=True,
    linecolor="black",
    linewidth=1,
)
fig.update_traces(marker_color="#3D81F6", marker_line_width=0)
fig.update_layout(
    plot_bgcolor='white',
    paper_bgcolor='white',
    margin=dict(l=60, r=60, t=60, b=60),
    width=700,
    font=dict(
        family="Palatino Linotype, Palatino, serif",
        color="black"
    )
)
fig.show(renderer='png', scale=3)

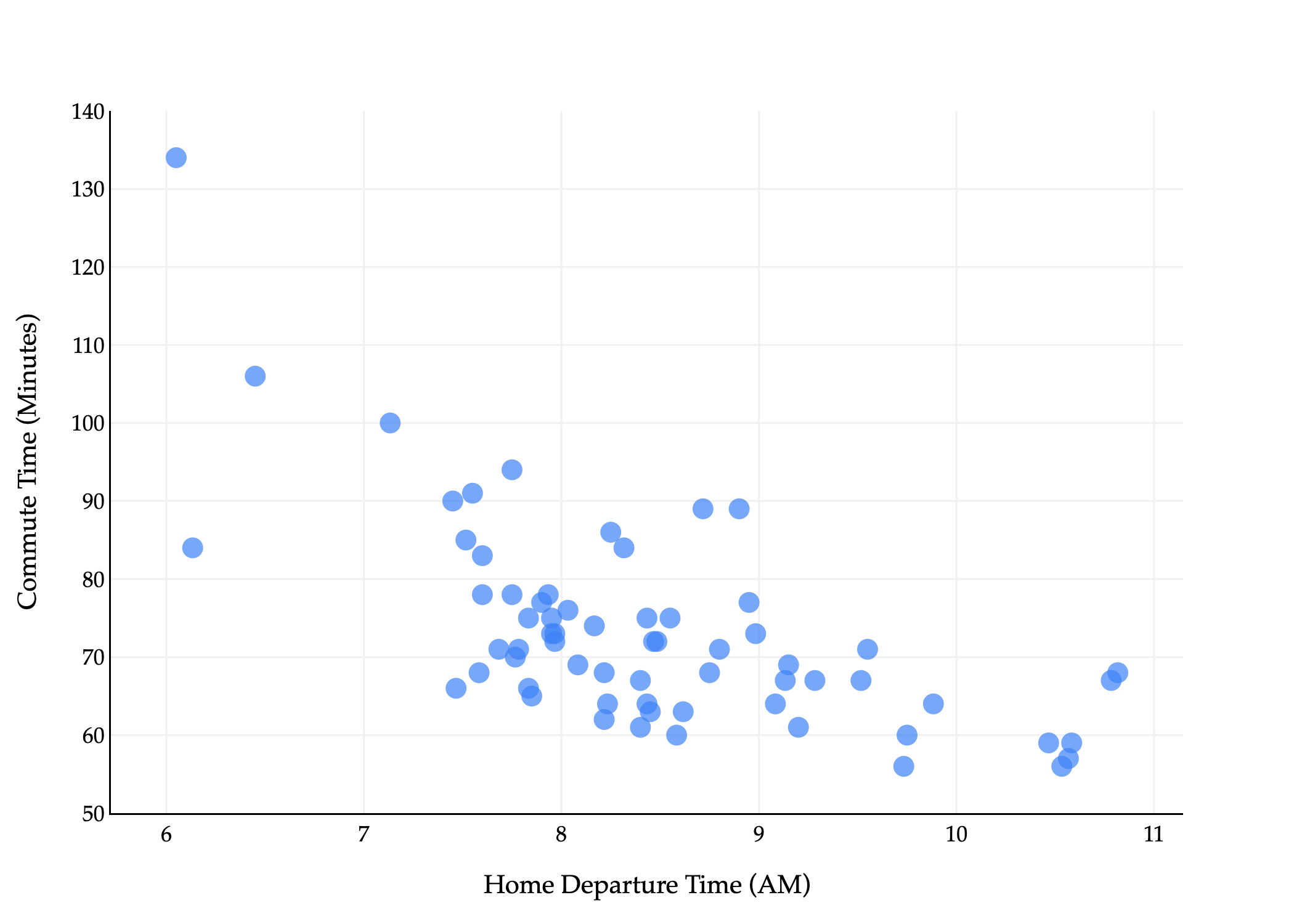
More to come! We’ll cover this example on Tuesday, and talk more about convexity (and, time permitting, variants of gradient descent for large datasets).