Skip to article frontmatterSkip to article content
Site not loading correctly?

This may be due to an incorrect BASE_URL configuration. See the MyST Documentation for reference.

9.5. Symmetric Matrices and the Spectral Theorem

Symmetric matrices – that is, square matrices where A=ATA = A^T – behave really nicely through the lens of eigenvectors, and understanding exactly how they work is key to Chapter 10.1, when we generalize beyond square matrices.

If you search for the spectral theorem online, you’ll often just see Statement 4 above; I’ve broken the theorem into smaller substatements to see how they are chained together.

Orthogonal matrices QQ satisfy QTQ=QQT=IQ^TQ = QQ^T = I, meaning their columns (and rows) are orthonormal, not just orthogonal to one another. The fact that QTQ=QQT=IQ^TQ = QQ^T = I means that QT=Q−1Q^T = Q^{-1}, so taking the transpose of a matrix is the same as taking its inverse.

So, instead of

A=VΛV−1A = V \Lambda V^{-1}

we’ve “upgraded” to

A=QΛQTA = Q \Lambda Q^T

This is the main takeaway of the spectral theorem: that symmetric matrices can be diagonalized by an orthogonal matrix. Sometimes, A=QΛQTA = Q \Lambda Q^T is called the spectral decomposition of AA, but all it is is a special case of the eigenvalue decomposition for symmetric matrices.

Visualizing the Spectral Theorem

Why do we prefer QΛQTQ \Lambda Q^T over VΛV−1V \Lambda V^{-1}? Taking the transpose of a matrix is much easier than inverting it, so actually working with QΛQTQ \Lambda Q^T is easier.

A=QΛQT  ⟹  Ak=QΛkQT⏟no inversion needed!\underbrace{A = Q \Lambda Q^T \implies A^k = Q \Lambda^k Q^T}_{\text{no inversion needed!}}

But it’s also an improvement in terms of interpretation: remember that orthogonal matrices are matrices that represent rotations. So, if AA is symmetric, then the linear transformation f(x⃗)=Ax⃗f(\vec x) = A \vec x is a sequence of rotations and stretches.

f(x⃗)=Ax⃗=QΛQTx⃗f(\vec x) = A \vec x = Q \Lambda Q^T \vec x

Let’s make sense of this visually. Consider the symmetric matrix A=[1221]A = \begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}.

We now focus on symmetric matrices and the spectral theorem.

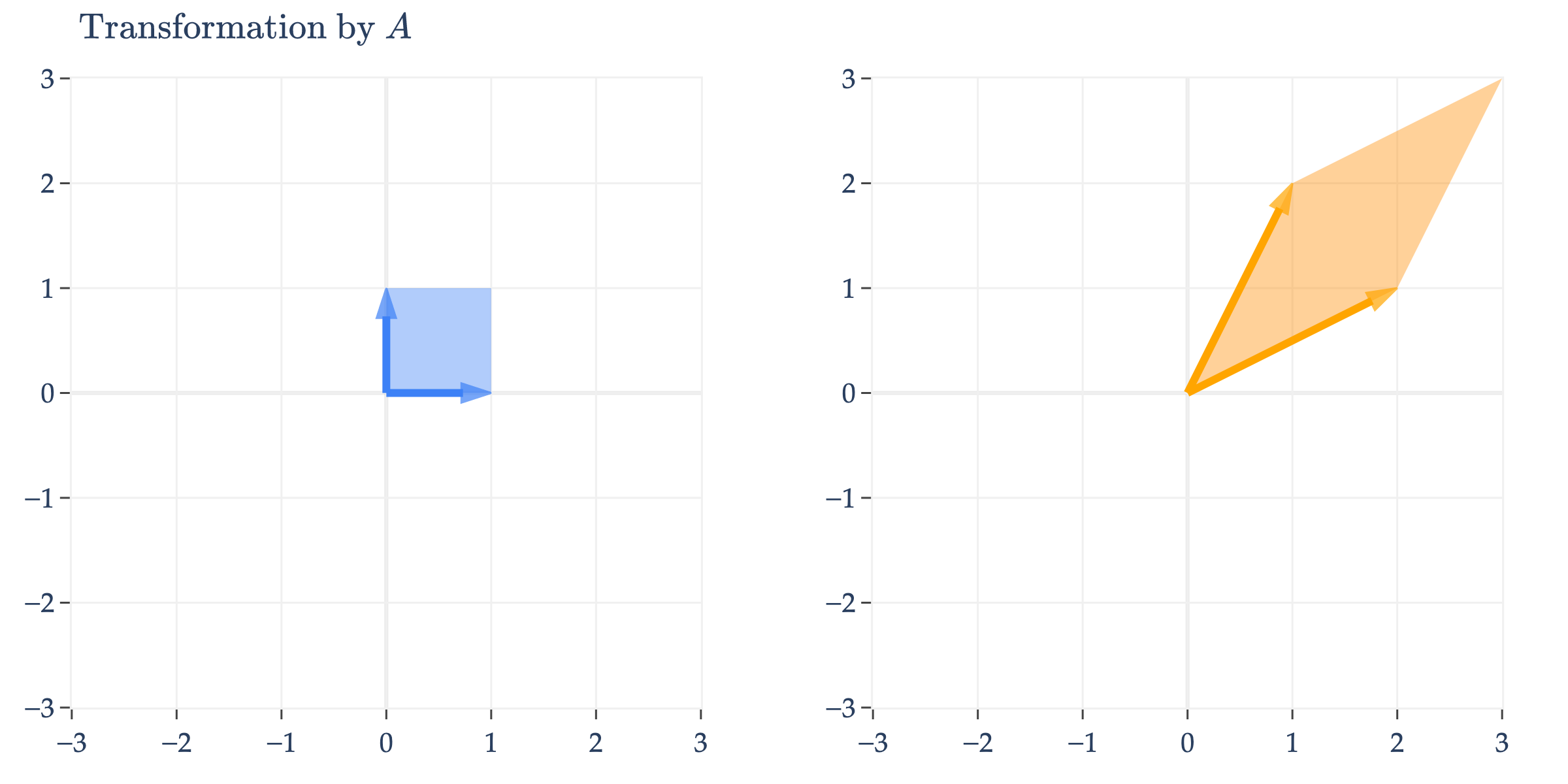
Image produced in Jupyter

AA appears to perform an arbitrary transformation; it turns the unit square into a parallelogram, as we first saw in Chapter 6.1.

But, since AA is symmetric, it can be diagonalized by an orthogonal matrix, A=QΛQTA = Q \Lambda Q^T.

A=[1221]A = \begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}

has eigenvalues λ1=3\lambda_1 = 3 with eigenvector v⃗1=[11]\vec v_1 = \begin{bmatrix} 1 \\ 1 \end{bmatrix} and λ2=−1\lambda_2 = -1 with eigenvector v⃗2=[−11]\vec v_2 = \begin{bmatrix} -1 \\ 1 \end{bmatrix}. But, the v⃗i\vec v_i’s I’ve written aren’t unit vectors, which they need to be in order for QQ to be orthogonal. So, we normalize them to get q⃗1=[1212]\vec q_1 = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} and q⃗2=[−1212]\vec q_2 = \begin{bmatrix} -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix}. Placing these q⃗i\vec q_i’s as columns of QQ, we get

Q=[12−121212]Q = \begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix}

and so

A=QΛQT=[12−121212]⏟Q[300−1]⏟Λ[1212−1212]⏟QTA = Q \Lambda Q^T = \underbrace{\begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix}}_Q \underbrace{\begin{bmatrix} 3 & 0 \\ 0 & -1 \end{bmatrix}}_\Lambda \underbrace{\begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix}}_{Q^T}

We’re visualizing how x⃗\vec x turns into Ax⃗A \vec x, i.e. how x⃗\vec x turns into QΛQTx⃗Q \Lambda Q^T \vec x. This means that we first need to consider the effect of QTQ^T on x⃗\vec x, then the effect of Λ\mathcal{\Lambda} on that result, and finally the effect of QQ on that result – that is, read the matrices from right to left.

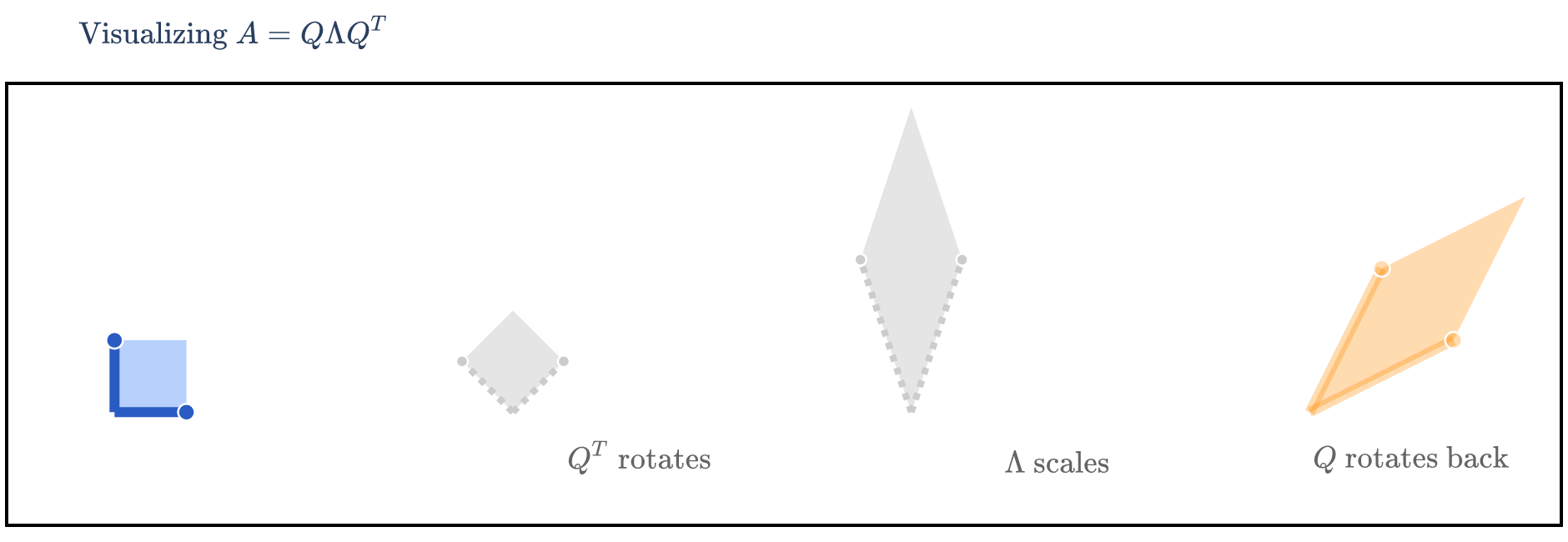
Image produced in Jupyter

The Ellipse Perspective

Another way of visualizing the linear transformation of a symmetric matrix is to consider its effect on the unit circle, not the unit square. Below, I’ll apply A=[1221]A = \begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix} to the unit circle.

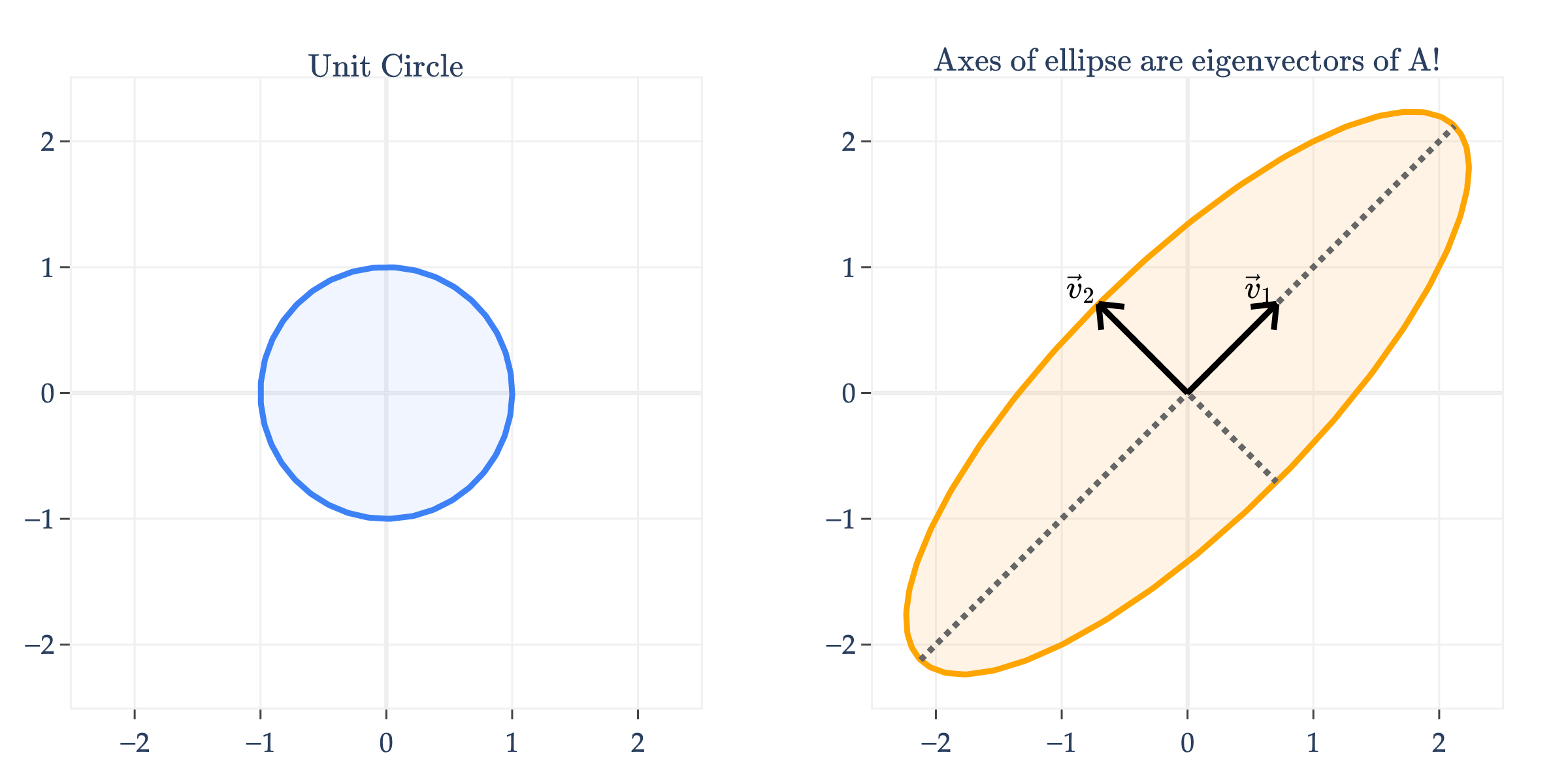
Image produced in Jupyter

Notice that AA transformed the unit circle into an ellipse. What’s more, the axes of the ellipse are the eigenvector directions of AA!

Why is one axis longer than the other? As you might have guessed, the longer axis – the one in the direction of the eigenvector v⃗1=[11]\vec v_1 = \begin{bmatrix} 1 \\ 1 \end{bmatrix} – corresponds to the larger eigenvalue. Remember that AA has λ1=3\lambda_1 = 3 and λ2=−1\lambda_2 = -1, so the “up and to the right” axis is three times longer than the “down and to the right” axis, defined by v⃗2=[1−1]\vec v_2 = \begin{bmatrix} 1 \\ -1 \end{bmatrix}.

To see why this happens, consult the solutions to Lab 11, Activity 6b to try and derive it. It has to do with the expression ∑i=1nλiyi2\sum_{i = 1}^n \lambda_i y_i^2’s in that derivation. What are the λi\lambda_i’s and where did the yiy_i’s come from?

Positive Semidefinite Matrices

I will keep this section brief; this is mostly meant to be a reference for a specific definition that you used in Lab 11 and will use in Homework 10.

What does this have anything to do with the diagonalization of a matrix? We just spent a significant amount of time talking about the special properties of symmetric matrices, and positive semidefinite matrices are a subset of symmetric matrices, so the properties implied by the spectral theorem also apply to positive semidefinite matrices.

Positive semidefinite matrices appear in the context of minimizing quadratic forms, f(x⃗)=x⃗TAx⃗f(\vec x) = \vec x^T A \vec x. You’ve toyed around with this in Lab 11, but also note that in Chapter 8.1 we saw the most important quadratic form of all: the mean-squared error!

Rsq(w⃗)=1n∥y⃗−Xw⃗∥2⏟this involves a quadratic form\underbrace{R_\text{sq}(\vec w) = \frac{1}{n} \lVert \vec y - X \vec w \rVert^2}_{\text{this involves a quadratic form}}

If we know all of the eigenvalues of AA in x⃗TAx⃗\vec x^T A \vec x are non-negative, then we know that x⃗TAx⃗≥0\vec x^T A \vec x \geq 0 for all x⃗\vec x, meaning that the quadratic form has a global minimum. This is why, as discussed in Lab 11, the quadratic form x⃗TAx⃗\vec x^T A \vec x is convex if and only if AA is positive semidefinite.

The fact that having non-negative eigenvalues implies the first definition of positive semidefiniteness is not immediately obvious, but is exactly what we proved in Lab 11, Activity 6.

A positive definite matrix is one in which x⃗TAx⃗>0\vec x^T A \vec x > 0 for all x⃗≠0⃗\vec x \neq \vec 0, i.e. where all eigenvalues are positive, not just non-negative (0 is no longer an option).

Key Takeaways

  1. The eigenvalue decomposition of a matrix AA is a decomposition of the form

    A=VΛV−1A = V \Lambda V^{-1}

    where VV is a matrix containing the eigenvectors of AA as columns, and Λ\mathcal{\Lambda} is a diagonal matrix of eigenvalues in the same order. Only diagonalizable matrices can be decomposed in this way.

  2. The algebraic multiplicity of an eigenvalue λi\mathbf{\lambda}_i is the number of times λi\mathbf{\lambda}_i appears as a root of the characteristic polynomial of AA.

  3. The geometric multiplicity of λ\mathbf{\lambda} is the dimension of the eigenspace of λ\mathbf{\lambda}, i.e. dim(nullsp(A−λI))\text{dim}(\text{nullsp}(A - \lambda I)).

  4. The n×nn \times n matrix is diagonalizable if and only if any of these equivalent conditions are true:

    • AA has nn linearly independent eigenvectors.

    • For every eigenvalue λi\lambda_i, GM(λi)=AM(λi)\text{GM}(\lambda_i) = \text{AM}(\lambda_i).

    • AA has nn distinct eigenvalues.

    When AA is diagonalizable, it has an eigenvalue decomposition, A=VΛV−1A = V \Lambda V^{-1}.

  5. If AA is a symmetric matrix, then the spectral theorem tells us that AA can be diagonalized by an orthogonal matrix QQ such that

    A=QΛQTA = Q \Lambda Q^T

    and that all of AA’s eigenvalues are guaranteed to be real.

What’s next? There’s the question of how any of this relates to real data. Real data comes in rectangular matrices, not square matrices. And even it were square, how does any of this enlighten us?

Chapter 9: Eigenvalues and Eigenvectors
9.4. Multiplicities and Diagonalization
Chapter 10: Singular Value Decomposition
10.1. Computing the Singular Value Decomposition