Skip to article frontmatterSkip to article content
Site not loading correctly?

This may be due to an incorrect BASE_URL configuration. See the MyST Documentation for reference.

2.3. Finding Optimal Parameters

Finding the Partial Derivatives

Let’s return to the simple linear regression problem. Recall, the function we’re trying to minimize is:

Rsq(w0,w1)=1n∑i=1n(yi−(w0+w1xi))2R_\text{sq}(w_0, w_1) = \frac{1}{n} \sum_{i=1}^n (y_i - (w_0 + w_1 x_i))^2

Why? By minimizing Rsq(w0,w1)R_\text{sq}(w_0, w_1), we’re finding the intercept (w0∗w_0^*) and slope (w1∗w_1^*) of the line that best fits the data. Don’t forget that this goal is the point of all of these mathematical ideas.

Using partial derivatives from the detour, we now minimize mean squared error to find the optimal parameters.

Loading...

We’ve learned that to minimize Rsq(w0,w1)R_\text{sq}(w_0, w_1), we’ll need to find both of its partial derivatives, and solve for the point (w0∗,w1∗,Rsq(w0∗,w1∗))(w_0^*, w_1^*, R_\text{sq}(w_0^*, w_1^*)) at which they’re both 0.

Let’s start with the partial derivative with respect to w0w_0:

Rsq(w0,w1)=1n∑i=1n(yi−(w0+w1xi))2∂Rsq∂w0=∂∂w0[1n∑i=1n(yi−(w0+w1xi))2]=1n∑i=1n∂Rsq∂w0(yi−(w0+w1xi))2=1n∑i=1n2(yi−(w0+w1xi))⋅∂Rsq∂w0(yi−(w0+w1xi))⏟chain rule=1n∑i=1n2(yi−(w0+w1xi))⋅(−1)=−2n∑i=1n(yi−(w0+w1xi))\begin{align*} R_\text{sq}(w_0, w_1) &= \frac{1}{n} \sum_{i = 1}^n (y_i - (w_0 + w_1 x_i))^2 \\ \frac{\partial R_{\text{sq}}}{\partial w_0} &= \frac{\partial}{\partial w_0} \left[ \frac{1}{n} \sum_{i = 1}^n (y_i - (w_0 + w_1 x_i))^2 \right] \\ &=\frac{1}{n} \sum_{i = 1}^n\frac{\partial R_{\text{sq}}}{\partial w_0} \left( y_i-(w_0+w_1 x_i) \right)^2 \\ &=\frac{1}{n} \sum_{i = 1}^n 2( y_i-(w_0+w_1 x_i) ) \cdot \underbrace{\frac{\partial R_{\text{sq}}}{\partial w_0}( y_i-(w_0+w_1 x_i) )}_\text{chain rule} \\ &=\frac{1}{n} \sum_{i = 1}^n 2( y_i-(w_0+w_1 x_i) ) \cdot (-1) \\ &=-\frac{2}{n} \sum_{i = 1}^n( y_i-(w_0+w_1 x_i) ) \end{align*}

Onto w1w_1:

Rsq(w0,w1)=1n∑i=1n(yi−(w0+w1xi))2∂Rsq∂w1=∂∂w1[1n∑i=1n(yi−(w0+w1xi))2]=1n∑i=1n∂Rsq∂w1(yi−(w0+w1xi))2=1n∑i=1n2(yi−(w0+w1xi))⋅∂Rsq∂w1(yi−(w0+w1xi))⏟chain rule=1n∑i=1n2(yi−(w0+w1xi))⋅(−xi)=−2n∑i=1nxi(yi−(w0+w1xi))\begin{aligned} R_\text{sq}(w_0, w_1) &= \frac{1}{n} \sum_{i = 1}^n (y_i - (w_0 + w_1 x_i))^2 \\ \frac{\partial R_{\text{sq}}}{\partial w_1} &= \frac{\partial}{\partial w_1} \left[ \frac{1}{n} \sum_{i = 1}^n (y_i - (w_0 + w_1 x_i))^2 \right] \\ &=\frac{1}{n} \sum_{i = 1}^n\frac{\partial R_{\text{sq}}}{\partial w_1} \left( y_i-(w_0+w_1 x_i) \right)^2 \\ &=\frac{1}{n} \sum_{i = 1}^n 2( y_i-(w_0+w_1 x_i) ) \cdot \underbrace{\frac{\partial R_{\text{sq}}}{\partial w_1}( y_i-(w_0+w_1 x_i) )}_\text{chain rule} \\ &=\frac{1}{n} \sum_{i = 1}^n 2( y_i-(w_0+w_1 x_i) ) \cdot (-x_i) \\ &=-\frac{2}{n} \sum_{i = 1}^n x_i( y_i-(w_0+w_1 x_i) ) \end{aligned}

All in one place now:

∂Rsq∂w0=−2n∑i=1n(yi−(w0+w1xi))∂Rsq∂w1=−2n∑i=1nxi(yi−(w0+w1xi))\begin{aligned} &\frac{\partial R_{\text{sq}}}{\partial w_0} = -\frac{2}{n} \sum_{i = 1}^n( y_i-(w_0+w_1 x_i) ) \\ &\frac{\partial R_{\text{sq}}}{\partial w_1} = -\frac{2}{n} \sum_{i = 1}^n x_i( y_i-(w_0+w_1 x_i) ) \end{aligned}

These look very similar – it’s just ∂Rsq∂w1\frac{\partial R_{\text{sq}}}{\partial w_1} has an added xix_i in the summation.

Remember, both partial derivatives are functions of two variables: w0w_0 and w1w_1. We’re treating the xix_i’s and yiy_i’s as constants. If I already have a dataset, you can pick an intercept w0w_0 and slope w1w_1 and I can use these formulas to compute the partial derivatives of RsqR_\text{sq} for that combination of intercept and slope.

In case it helps you put things in perspective, here’s how I might implement these formulas in code, assuming that x and y are arrays:

# Assume x and y are defined somewhere above this function.
def partial_R_w0(w0, w1):
    # Sub-optimal technique, since it uses a for-loop.
    total = 0
    for i in range(len(x)):
        total += (y[i] - (w0 + w1 * x[i]))
    return -2 * total / len(x)
    # Returns a single number!

def partial_R_w1(w0, w1):
    # Better technique, as it uses vectorized operations.
    return -2 * np.mean(x * (y - (w0 + w1 * x)))
    # Also returns a single number!

Before we solve for where both ∂Rsq∂w0\frac{\partial R_{\text{sq}}}{\partial w_0} and ∂Rsq∂w1\frac{\partial R_{\text{sq}}}{\partial w_1} are 0, let’s visualize them in the context of our loss surface.

Loading...

Click “Slider for values of w0w_0”. No matter where you drag that slider, the resulting gold curve is a function of w1w_1 only. Every gold curve you see when dragging the w0w_0 slider will have a minimum at some value of w1w_1.

Then, click “Slider for values of w1w_1”. No matter where you drag that slider, the resulting gold curve is a function of w0w_0 only, and has some minimum value.

But there is only one combination of w0w_0 and w1w_1 where the gold curves have minimums at the exact same intersecting point. That is the combination of w0w_0 and w1w_1 that minimizes RsqR_\text{sq}, and it’s who we’re searching for.

Solving for the Optimal Parameters

Now, it’s time to analytically (that is, on paper) find the values of w0∗w_0^* and w1∗w_1^* that minimize RsqR_\text{sq}. We’ll do so by solving the following system of two equations and two unknowns:

∂Rsq∂w0=−2n∑i=1n(yi−(w0+w1xi))=0∂Rsq∂w1=−2n∑i=1nxi(yi−(w0+w1xi))=0\begin{aligned} \frac{\partial R_\text{sq}}{\partial w_0} &= -\frac{2}{n} \sum_{i = 1}^n( y_i-(w_0+w_1 x_i) )=0 \\ \frac{\partial R_\text{sq}}{\partial w_1} &= -\frac{2}{n} \sum_{i = 1}^n x_i( y_i-(w_0+w_1 x_i) )=0 \end{aligned}

Here’s my plan:

  1. In the first equation, try and isolate for w0w_0; this value will be called w0∗w_0^*.

  2. Plug the expression for w0∗w_0^* into the second equation to solve for w1∗w_1^*.

Let’s start with the first step.

−2n∑i=1n(yi−(w0+w1xi))=0-\frac{2}{n} \sum_{i = 1}^n( y_i-(w_0+w_1 x_i) )=0

Multiplying both sides by −n2-\frac{n}{2} gives us:

∑i=1n(yi⏟actual−w0+w1xi⏟predicted)=0\sum_{i = 1}^n( \underbrace{y_i}_\text{actual}-\underbrace{w_0+w_1 x_i}_\text{predicted})=0

Before I continue, I want to highlight that this itself is an importance balance condition, much like those we discussed in Chapter 1.3. It’s saying that the sum of the errors of the optimal line’s predictions – that is, the line with intercept w0∗w_0^* and slope w1∗w_1^* – is 0.

Let’s continue with the first step – I’ll try and keep the commentary to a minimum. It’s important to try and replicate these steps yourself, on paper.

∑i=1n(yi−(w0+w1xi))=0∑i=1n(yi−w0−w1xi)=0∑i=1nyi−∑i=1nw0−∑i=1nw1xi=0∑i=1nyi−nw0−w1∑i=1nxi=0∑i=1nyi−w1∑i=1nxi=nw0∑i=1nyin−w1∑i=1nxin=w0w0∗=yˉ−w1∗xˉ\begin{aligned} \sum_{i = 1}^n( y_i-(w_0+w_1 x_i) )&=0 \\ \sum_{i = 1}^n( y_i-w_0-w_1 x_i )&=0 \\ \sum_{i = 1}^n y_i - \sum_{i = 1}^n w_0 - \sum_{i = 1}^n w_1 x_i&=0 \\ \sum_{i = 1}^n y_i - nw_0 - w_1\sum_{i = 1}^n x_i&=0\\ \sum_{i = 1}^n y_i - w_1\sum_{i = 1}^n x_i&=nw_0 \\ \frac{\sum_{i = 1}^n y_i }{n}- w_1\frac{\sum_{i = 1}^n x_i}{n}&=w_0 \\ w_0^*&=\bar{y}-w_1^* \bar{x} \end{aligned}

Awesome! We’re halfway there. We have a formula for the optimal slope, w0∗w_0^*, in terms of the optimal intercept, w1∗w_1^*. Let’s use w0∗=yˉ−w1∗xˉw_0^* = \bar{y}-w_1^* \bar{x} and see where it gets us in the second equation.

−2n∑i=1nxi(yi−(w0+w1xi))=0∑i=1nxi(yi−(w0+w1xi))=0∑i=1nxi(yi−(yˉ−w1∗xˉ⏟w0∗+w1∗xi))=0∑i=1nxi(yi−yˉ+w1∗xˉ−w1∗xi⏟distribute negation)=0∑i=1nxi((yi−yˉ)−w1∗(xi−xˉ))=0∑i=1nxi(yi−yˉ)−w1∗∑i=1nxi(xi−xˉ)⏟expand summation=0∑i=1nxi(yi−yˉ)=w1∗∑i=1nxi(xi−xˉ)w1∗=∑i=1nxi(yi−yˉ)∑i=1nxi(xi−xˉ)\begin{aligned} -\frac{2}{n} \sum_{i = 1}^n x_i( y_i-(w_0+w_1 x_i) )&=0 \\ \sum_{i = 1}^n x_i( y_i-(w_0+w_1 x_i) )&=0 \\ \sum_{i = 1}^n x_i( y_i-(\underbrace{\bar{y}-w_1^* \bar{x}}_{w_0^*}+w_1^* x_i) )&=0 \\ \sum_{i = 1}^n x_i( \underbrace{y_i-\bar{y}+w_1^* \bar{x}-w_1^* x_i}_\text{distribute negation})&=0 \\ \sum_{i = 1}^n x_i \left( (y_i-\bar{y})-w_1^* ( x_i - \bar{x}) \right) &=0 \\ \underbrace{\sum_{i = 1}^n x_i (y_i-\bar{y})-w_1^* \sum_{i=1}^n x_i ( x_i - \bar{x})}_\text{expand summation} &=0 \sum_{i = 1}^n x_i (y_i-\bar{y}) &= w_1^* \sum_{i=1}^n x_i ( x_i - \bar{x}) \\ w_1^* &= \frac{\sum_{i = 1}^n x_i (y_i-\bar{y})}{\sum_{i=1}^n x_i ( x_i - \bar{x})} \end{aligned}

Rewriting and Using the Formulas

We’re done! We have formulas for the optimal slope and intercept. But, before we celebrate, I’m going to try and rewrite w1∗w_1^* in an equivalent, more symmetrical form that is easier to interpret.

Claim:

w1∗=∑i=1nxi(yi−yˉ)∑i=1nxi(xi−xˉ)⏟formula we derived above=∑i=1n(xi−xˉ)(yi−yˉ)∑i=1n(xi−xˉ)2⏟nicer looking formulaw_1^* = \underbrace{\frac{\sum_{i = 1}^n x_i (y_i-\bar{y})}{\sum_{i=1}^n x_i ( x_i - \bar{x})}}_\text{formula we derived above} = \underbrace{\frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2}}_\text{nicer looking formula}
Proof of equivalent, nicer looking formula

To show that these two formulas are equal, I’ll start by recapping the fact that the sum of deviations from the mean is 0, in other words:

∑i=1n(xi−xˉ)=0\sum_{i=1}^n (x_i - \bar{x}) = 0

This has come up in homeworks and past sections of the notes, but for completeness, here’s the proof:

∑i=1nxi−xˉ∑i=1nxi−∑i=1nxˉ=nxˉ−nxˉ=0\begin{aligned} &\sum_{i = 1}^n x_i - \bar{x} \\ &\sum_{i = 1}^n x_i - \sum_{i = 1}^n \bar{x} \\ &=n \bar{x} - n \bar{x} \\ &=0 \end{aligned}

Equipped with this fact, I can show that the new, more symmetric version of the formula is equal to the original one I derived.

new formula for w1∗=∑i=1n(xi−xˉ)(yi−yˉ)∑i=1n(xi−xˉ)2original formula for w1∗=∑i=1nxi (yi−yˉ)∑i=1nxi (xi−xˉ)numerator of new formula: ∑i=1n(xi−xˉ)(yi−yˉ)=∑i=1n(xi(yi−yˉ)−xˉ(yi−yˉ))=∑i=1nxi(yi−yˉ)−∑i=1nxˉ(yi−yˉ)=∑i=1nxi(yi−yˉ)−xˉ∑i=1n(yi−yˉ)⏟=0=∑i=1nxi(yi−yˉ)=numerator of original formula!denominator of new formula: ∑i=1n(xi−xˉ)2=∑i=1n(xi−xˉ)(xi−xˉ)=∑i=1nxi(xi−xˉ)−xˉ∑i=1n(xi−xˉ)⏟same logic as in the denominator case=∑i=1nxi(xi−xˉ)=denominator of original formula!\begin{align*} \text{new formula for } w_1^* &= \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2} \\[6pt] \text{original formula for } w_1^* &= \frac{\displaystyle\sum_{i=1}^n x_i\,(y_i-\bar y)}{\displaystyle\sum_{i=1}^n x_i\,(x_i-\bar x)} \\[6pt] \text{numerator of new formula: } \quad &\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) \\ &=\sum_{i=1}^n \left( x_i(y_i - \bar{y}) - \bar{x} (y_i - \bar{y}) \right) \\ &=\sum_{i=1}^n x_i(y_i - \bar{y}) - \sum_{i=1}^n \bar{x}(y_i - \bar{y}) \\ &=\sum_{i=1}^n x_i(y_i - \bar{y}) - \bar{x} \underbrace{\sum_{i=1}^n (y_i - \bar{y})}_{=0} \\ &=\sum_{i=1}^n x_i(y_i - \bar{y}) \\ &=\text{numerator of original formula!} \\ \\ \\ \text{denominator of new formula: } \quad &\sum_{i=1}^n (x_i - \bar{x})^2 \\ &= \sum_{i=1}^n (x_i - \bar{x})(x_i - \bar{x}) \\ &= \sum_{i=1}^n x_i(x_i - \bar{x}) - \underbrace{\bar{x} \sum_{i=1^n} (x_i - \bar{x})}_\text{same logic as in the denominator case} \\ &= \sum_{i = 1}^n x_i (x_i - \bar{x}) \\ &= \text{denominator of original formula!} \end{align*}

We skipped some steps in the denominator case, since many of them are the same as in the numerator case. Nevertheless, since we’ve shown that the numerators of both formulas are the same and the denominators of both formulas are the same, well, both formulas are the same!

This is not the only other equivalent formula for the slope; for instance, w1∗=∑i=1n(xi−xˉ)yi∑i=1n(xi−xˉ)2w_1^* = \frac{\sum_{i=1}^n (x_i - \bar{x})y_i}{\sum_{i=1}^n (x_i - \bar{x})^2} too, and you can verify this using the same logic as in the proof above.

To summarize, the parameters that minimize mean squared error for the simple linear regression model, h(xi)=w0+w1xih(x_i) = w_0 + w_1 x_i, are:

w1∗=∑i=1n(xi−xˉ)(yi−yˉ)∑i=1n(xi−xˉ)2,w0∗=yˉ−w1∗xˉ\boxed{w_1^* = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2}, \qquad w_0^* = \bar{y} - w_1^* \bar{x}}

This is an important result, and you should remember it. There are a lot of symbols above, but just note that given a dataset (x1,y1),(x2,y2),…,(xn,yn)(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n), you could apply the formulas above by hand to find the optimal parameters yourself.

What does this line look like on the commute times data?

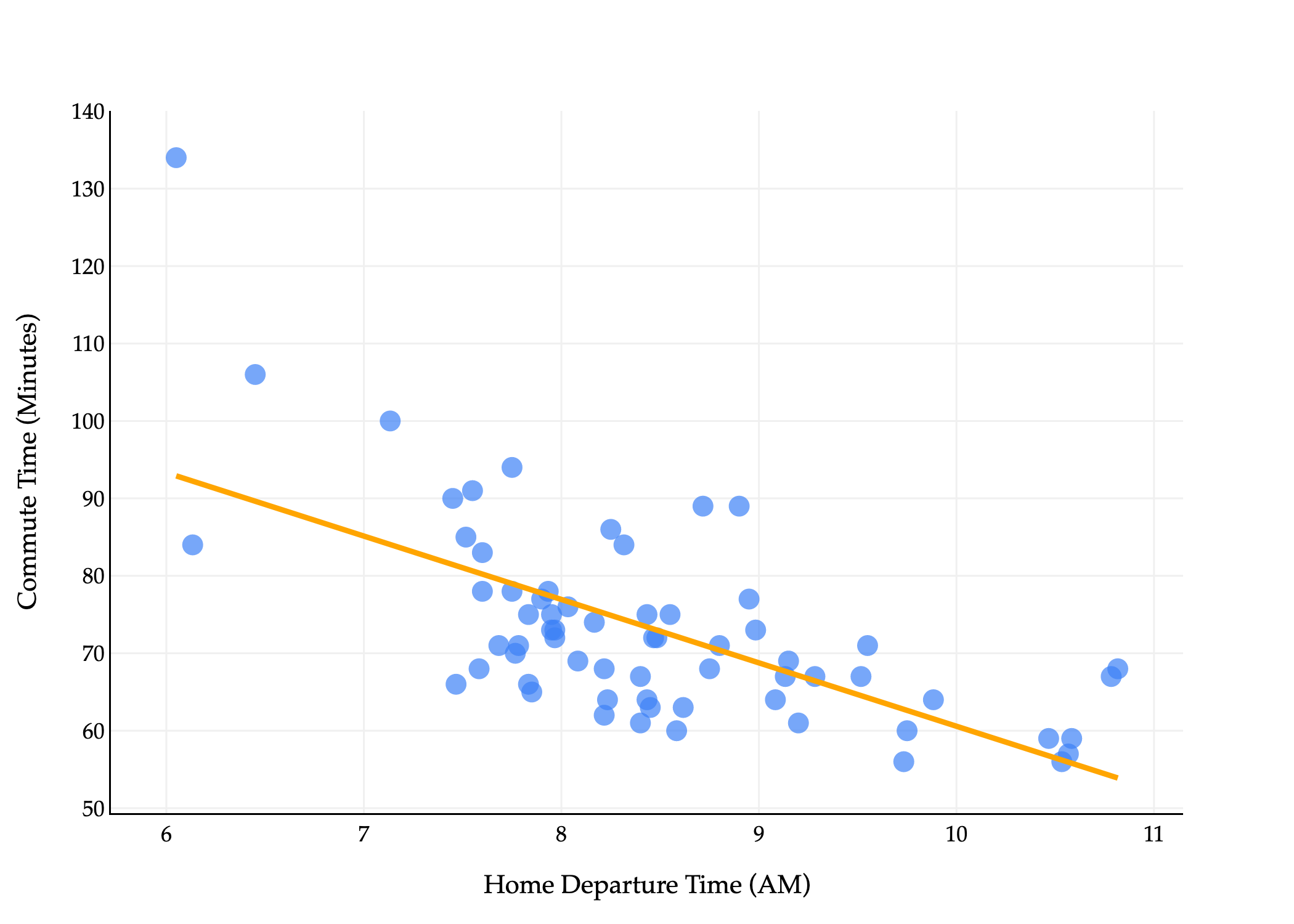
Image produced in Jupyter

The line above goes by many names:

  • The simple linear regression line that minimizes mean squared error.

  • The simple linear regression line (if said without context).

  • The regression line.

  • The least squares regression line (because it has the least mean squared error).

  • The line of best fit.

Whatever you’d like to call it, now that we’ve found our optimal parameters, we can use them to make predictions.

h(xi)=w0∗+w1∗xih(x_i) = w_0^* + w_1^* x_i

On the dataset of commute times:

# Assume x is an array with departure hours and y is an array with commute times.
w1_star = np.sum((x - np.mean(x)) * (y - np.mean(y))) / np.sum((x - np.mean(x)) ** 2)
w0_star = np.mean(y) - w1_star * np.mean(x)

w0_star, w1_star
(142.4482415877287, -8.186941724265552)

So, our specific fit, or trained hypothesis function is:

predicted commute timei=h(departure houri)=142.45−8.19⋅departure houri\begin{align*} \text{predicted commute time}_i &= h(\text{departure hour}_i) \\ &= 142.45 - 8.19 \cdot \text{departure hour}_i \end{align*}

This trained hypothesis function is not saying that leaving later causes you to have shorter commutes. Rather, that’s just the best linear pattern it observed in the data for the purposes of minimizing mean squared error. In reality, there are other factors that affect commute times, and we haven’t performed a thorough-enough analysis to say anything about the causal relationship between departure time and commute time.

To predict how long it might take to get to school tomorrow, plug in the time you’d like to leave for departure houri\text{departure hour}_i and out will come your prediction. The slope, -8.19, is in units units of yunits of x=minuteshour\frac{\text{units of } y}{\text{units of } x} = \frac{\text{minutes}}{\text{hour}}, and is telling us that for every hour later you leave, your predicted commute time decreases by 8.19 minutes.

In Python, I can define a predict function as follows:

def predict(x_new):
    return w0_star + w1_star * x_new

# Predicted commute time if I leave at 8:30AM.
predict(8.5)
72.8592369314715

Regression Line Passes Through the Mean

There’s an important property that the regression line satisfies: for any dataset, the line that minimizes mean squared error passes through the point (mean of x,mean of y)(\text{mean of } x, \text{mean of } y).

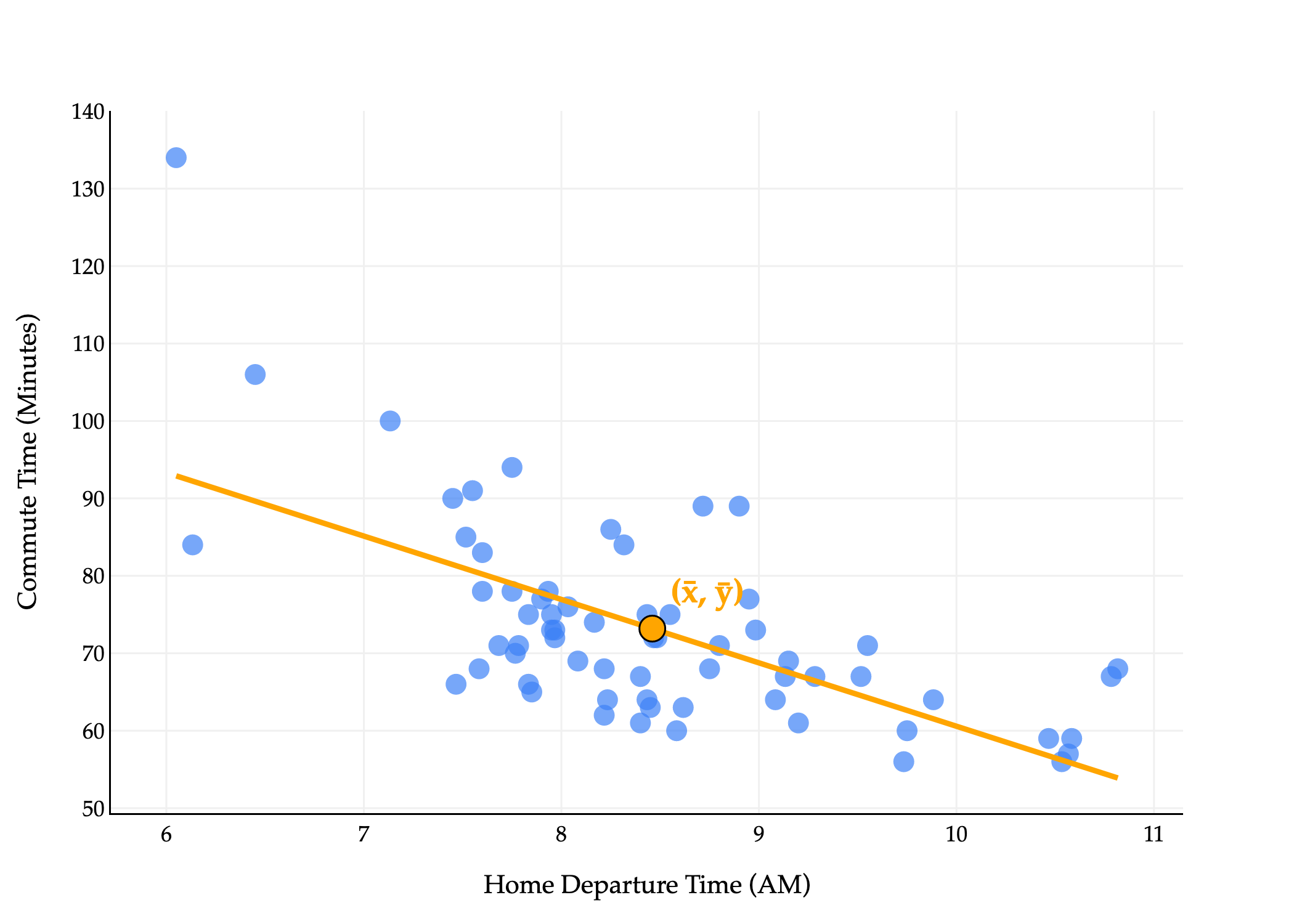
Image produced in Jupyter
predict(np.mean(x))
73.18461538461538
# Same!
np.mean(y)
73.18461538461538

Our commute times regression line passes through the point (xˉ,yˉ)(\bar{x}, \bar{y}), even if that was not necessarily one of the original points in the dataset.

Intuitively, this says that for an average input, the line that minimizes mean squared error will always predict an average output.

Why is this fact true? See if you can reason about it yourself, then check the solution once you’ve attempted it.

Proof that the regression line passes through (xˉ,yˉ)(\bar{x}, \bar{y})

Our regression line is:

h(xi)=w0∗+w1∗xih(x_i) = w_0^* + w_1^* x_i

We know that the optimal intercept of the regression line is:

w0∗=yˉ−w1∗xˉw_0^* = \bar{y} - w_1^* \bar{x}

Substituting this in yields:

h(xi)=yˉ−w1∗xˉ⏟w0∗+w1∗xih(x_i) = \underbrace{\bar{y} - w_1^* \bar{x}}_{w_0^*} + w_1^* x_i

If we plug in xi=xˉx_i = \bar{x}, we have:

h(xˉ)=yˉ −w1∗xˉ+w1∗xˉ⏟cancels out=yˉh(\bar{x}) = \bar{y} \: \underbrace{- w_1^* \bar{x} + w_1^* \bar{x}}_\text{cancels out} = \bar{y}

My interpretation of this is that the intercept is chosen to “vertically adjust” the line so that it passes through (xˉ,yˉ)(\bar{x}, \bar{y}).

The Modeling Recipe

To conclude, let’s run through the three-step modeling recipe.

1. Choose a model.

h(xi)=w0+w1xih(x_i) = w_0 + w_1 x_i

2. Choose a loss function.

We chose squared loss:

Lsq(yi,h(xi))=(yi−h(xi))2L_\text{sq}(y_i, h(x_i)) = (y_i - h(x_i))^2

3. Minimize average loss to find optimal parameters.

For the simple linear regression model, empirical risk is:

Rsq(w0,w1)=1n∑i=1n(yi−(w0+w1xi))2R_\text{sq}(w_0, w_1) = \frac{1}{n} \sum_{i=1}^n (y_i - (w_0 + w_1 x_i))^2

We showed that:

w1∗=∑i=1n(xi−xˉ)(yi−yˉ)∑i=1n(xi−xˉ)2,w0∗=yˉ−w1∗xˉw_1^* = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2}, \qquad w_0^* = \bar{y} - w_1^* \bar{x}

While the process of minimizing RsqR_\text{sq} was much, much more complex than in the case of our single parameter model, the conceptual backing of the process was still this three-step recipe, and hopefully now you see its value.

Having derived the optimal line, we next quantify how well a line fits data using correlation.

Chapter 2: Simple Linear Regression
2.2. Detour: Partial Derivatives
Chapter 2: Simple Linear Regression
2.4. Correlation